이번에 소개해드릴 내용은 시계열이나 신호 데이터에서 변화를 찾는 기법인 Change point detection입니다. 진행했던 프로젝트에서 공정 과정에서 유의미한 피처를 도출하기 위한 하나의 작업으로 Segmentation을 진행했고, Segmentation을 하기 위해 Change point detection 기법을 활용했습니다. 최종 목표는 유의미한 피처 도출이었고, 데이터의 변화가 발생한 구간을 나눠 보다 유의미한 피처를 도출하고자 하였습니다. 해당 글에서는 Change point detection 이 무엇인지, 어떻게 활용되는지, 알고리즘에는 어떤 것들이 있는지 간단한 실습과 함께 설명하고자 합니다.
1. CPD 개요
CPD(Change Point Detection)이란 시계열 데이터의 특성(평균, 분산, 분포 등) 변화를 통해 데이터가 변화하는 지점을 찾는 기법입니다. 갑작스럽게 주가가 올라가는 걸 탐지하거나 생체 데이터의 이상 변화를 감지하는 데 사용될 수도 있고, 산업 현장에서 문제가 생겼을 때 패턴 변화가 언제 발생했는지 찾아보기 위해 사용되기도 합니다. 데이터의 이상을 감지하기 위해서도 사용될 수 있지만 상태가 여러 번 변경되는 복잡한 시스템에서 신호를 분석하기 위해서도 사용됩니다. 예를 들어, 로봇의 센서 데이터나 인간의 생체 데이터에서는 다양한 동작을 포함하고 있기 때문에 이를 걷고, 뛰고, 멈춰 있는 상태 등으로 구분하는 작업이 필요합니다. 데이터를 수집하고 활용하는 어떤 분야던 데이터의 패턴이 변화한다는 것은 유의미한 신호이기 때문에 이를 분석하는 것은 매우 중요합니다.
2. CPD 알고리즘
Change point detection은 크게 실시간 데이터를 받아 변경 사항을 즉시 감지하는 온라인 방식과 모든 샘플이 확보된 과거 데이터에서 변화를 감지하는 오프라인 방식으로 나뉩니다. 흔히 온라인 방식은 Event Detection 혹은 Anomaly Detection으로도 불리며 오프라인 방식은 Signal Segmentation으로 불립니다. 프로젝트에서 진행했던 방식은 오프라인 방식이었기에 온라인은 간단히 소개만 드리고 오프라인을 집중해서 설명드리겠습니다.
(1) Online 모델
온라인 모델은 실시간 데이터 기반으로 변화점을 탐지하는 방식으로 스트리밍 환경에서 적용되기 때문에 미래 데이터가 없는 상태에서 즉각적인 변화 탐지가 가능해야 합니다. 관련 모델로는 CUSUM(Cumulative Sum Control Chart)과 Bayesian Online Change Point Detection, EWMA(Exponentially Weighted Moving Average) 등 통계적인 방법을 이용한 모델 등이 있으며 최근에는 AutoeEncoder와 같이 ML, DL 기반의 모델도 사용하고 있습니다. 여기서는 통계적 기법만 간단하게 설명드리겠습니다.
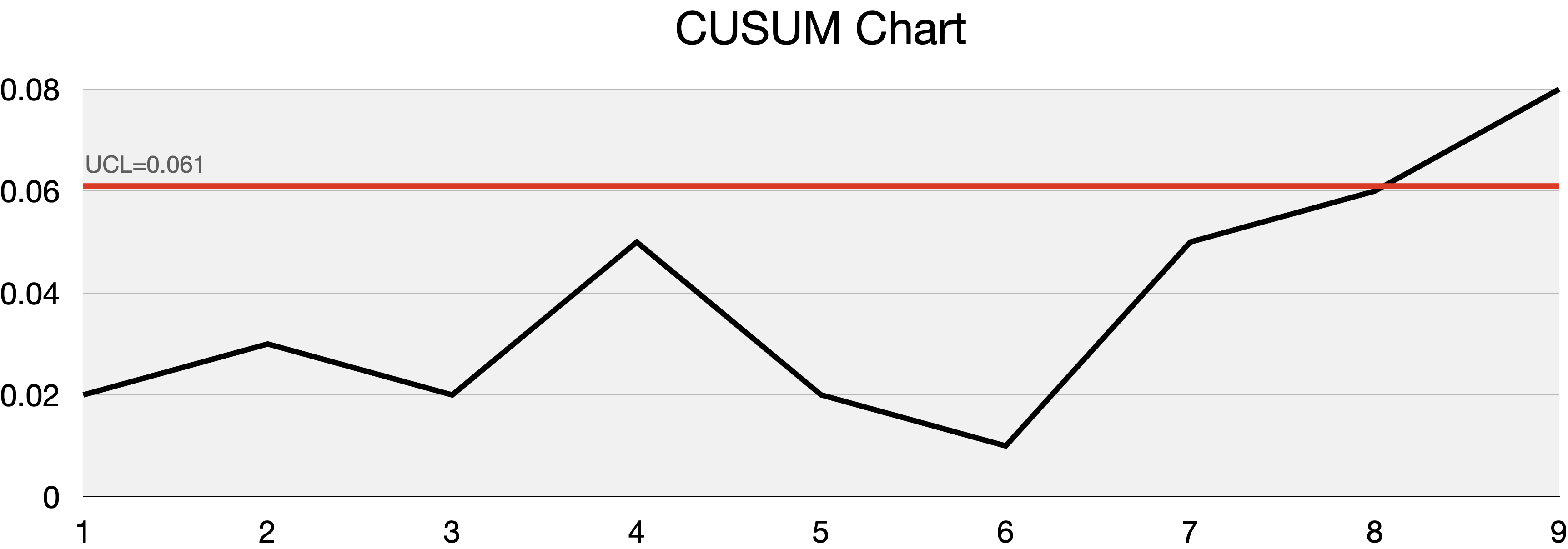
1) CUSUM (Cumulative Sum Control Chart)
CUSUM은 이름에서 알 수 있듯이 편차의 누적합을 사용해 변화점을 탐지하는 기법으로, 평균의 변화를 빠르게 탐지하여 점진적인 변화나 특정 값 이상의 변화가 발생할 때 유용합니다. 그렇기 때문에 산업 분야에서 미묘한 데이터의 변화를 감지해야 하는 공정 제어나 품질 관리를 위해 많이 사용되고 있습니다. 아래 그래프처럼 특정 시점의 데이터 포인트가 UCL(Upper Control Limit, 변화점 탐지를 위한 임계값)을 넘으면 데이터에 변화가 발생했다고 해석합니다.
2) Bayesian Online Change Point Detection
Bayesian Online Change Point Detection 의 경우 베이지안 확률 모델을 사용해 변화점의 발생 가능성을 실시간으로 계산합니다. 과거와 현재 데이터 간 사후 확률을 비교하여 변화 발생 가능성을 평가하기 때문에 계산 복잡도가 높은 편이지만 불확실성이 높은 상황에서 유용한 방법입니다.
3) EWMA (Exponentially Weighted Moving Average)
과거 데이터를 가중 평균하여 최근 데이터에 더 큰 가중치를 주는 방식으로 변화점을 탐지합니다. 노이즈가 많은 데이터의 변화에 유리하고 작은 프로세스 변화를 잘 감지하기 때문에 CUSUM과 함께 금융과 산업 분야에서 주로 사용됩니다.
(2) Offline 모델
오프라인 모델은 전체 데이터를 확보한 후 변화점을 탐지하는 방식으로 과거 데이터를 기반으로 탐지하기 때문에 보다 정확한 탐지가 가능합니다. 변화점 탐지 원리는 구간 간 차이를 정량화하도록 비용함수를 계산해 변화를 탐지합니다. 비용함수는 동질성의 척도로 구간 내 데이터가 유사할수록 비용함수가 낮게 나타납니다. 구간 별 비용함수를 계산해 비용함수가 커지게 되면 변화가 일어났다고 보고, 비용함수의 합이 최소화하도록 변화점을 찾아 같은 구간 내 유사한 데이터가 모이도록 구간을 나눕니다 .
데이터의 특성에 따라 알맞은 알고리즘과 비용함수를 선택해야 탐지 정확도를 높일 수 있으며 변화점 탐지에서 사용되는 비용함수는 아래 그림처럼 분류할 수 있습니다. 비용함수에 대한 자세한 내용을 알고 싶다면 Selective review of offline change point detection methods 논문을 참고해주세요.


1) PELT (Pruned Exact Linear Time)
최적화 기반의 알고리즘으로, 가지치기를 통해 정확한 변화점을 찾으면서도 계산 효율성을 높인 방법입니다. 이 알고리즘은 변화점 수를 사전에 알 필요가 없으며, 최적화 문제를 풀면서 정확한 변화점을 탐지할 수 있습니다. 시간복잡도가 선형으로 계산 효율성이 크다는 장점이 있어 큰 규모의 시계열 데이터에서 빠르게 변화점을 탐지해야 할 때 유용합니다.
import numpy as np
import matplotlib.pylab as plt
import ruptures as rpt
# creation of data
n, dim = 500, 3
n_bkps, sigma = 3, 1
signal, bkps = rpt.pw_constant(n, dim, n_bkps, noise_std=sigma)
# change point detection
model = "l1" # "l2", "rbf"
algo = rpt.Pelt(model=model, min_size=3, jump=5).fit(signal)
my_bkps = algo.predict(pen=3)
# show results
fig, ax_arr = rpt.display(signal, bkps, my_bkps, figsize=(10, 6))
plt.show()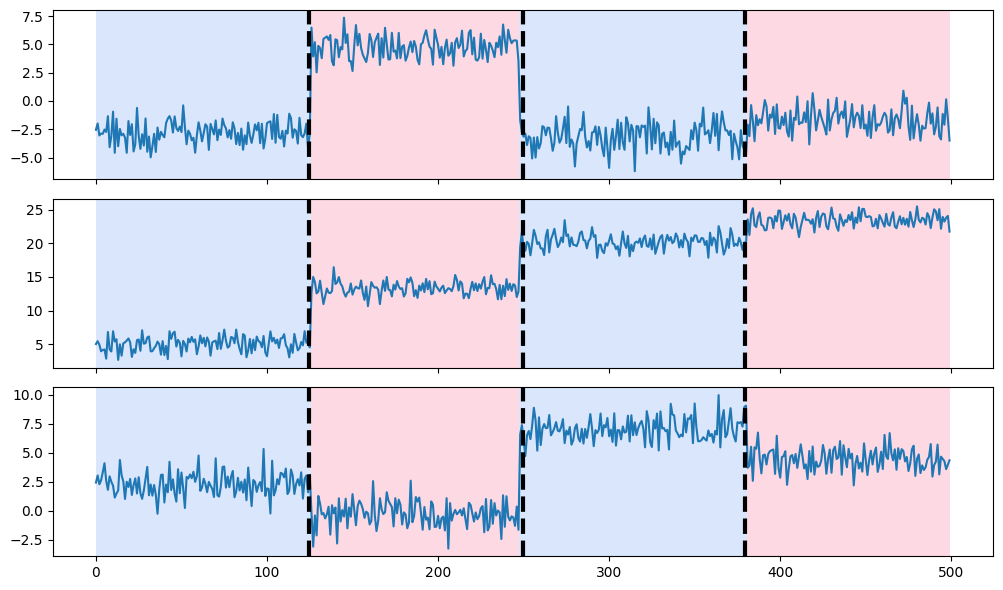
2) Binary Segmentation
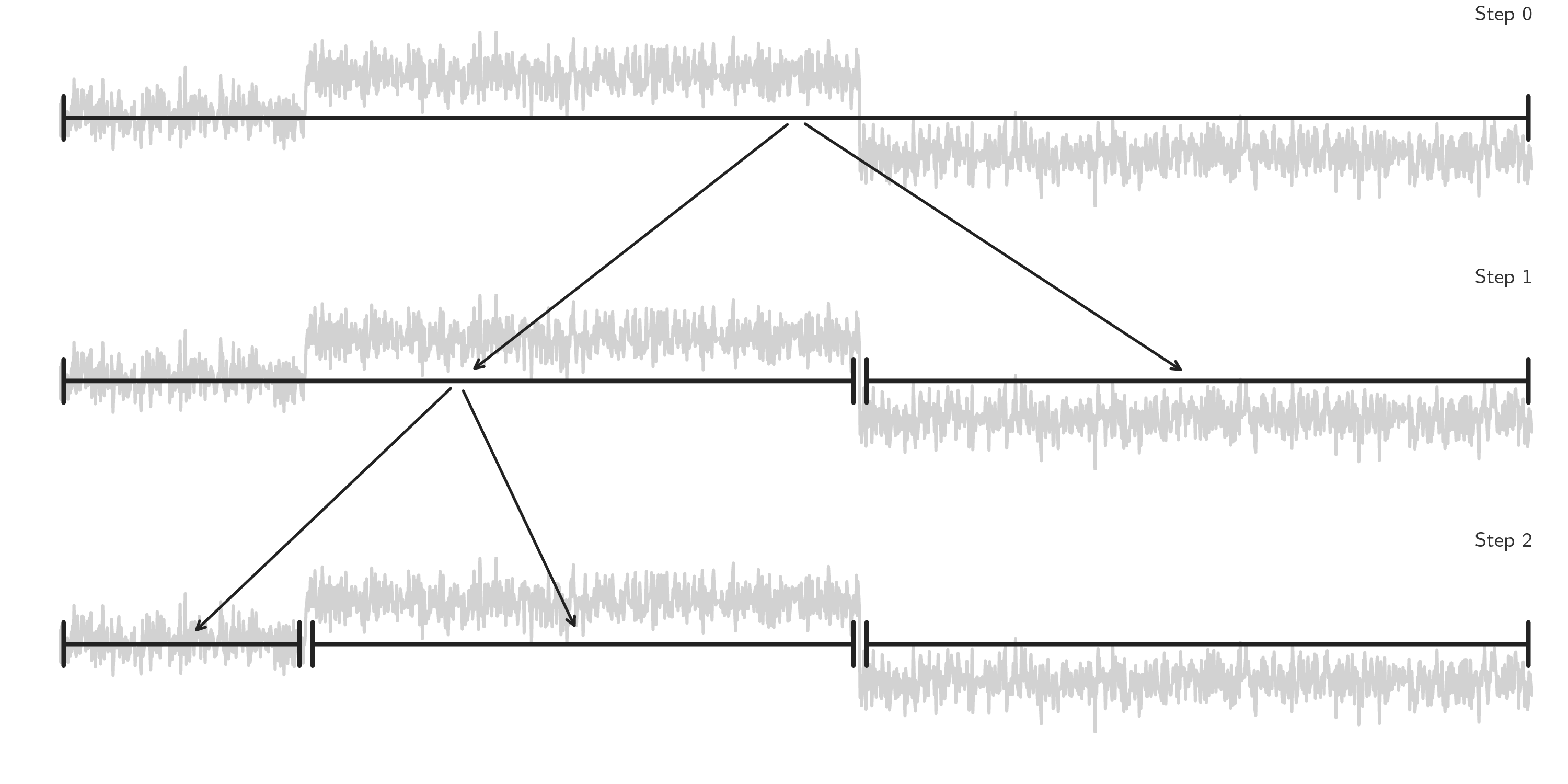
전체 시계열 데이터를 두 부분으로 나누고, 나눠진 두 개의 하위 신호에서 같은 작업은 반복하며 다시 변화점을 탐지하는 방식입니다. 가장 단순한 변화점 탐지 방법 중 하나로, 각 구간을 재귀적으로 분할하여 변화점을 찾습니다. 간단하고 직관적인 알고리즘이지만 여러 변화점이 동시에 존재할 때 정확도가 낮아질 수 있기 때문에 단순한 시계열 데이터에서 사용하는 것이 좋습니다.
import numpy as np
import matplotlib.pylab as plt
import ruptures as rpt
# creation of data
n = 500 # number of samples
n_bkps, sigma = 3, 1 # number of change points, noise standard deviation
signal, bkps = rpt.pw_constant(n, dim, n_bkps, noise_std=sigma)
# change point detection
model = "l2" # "l1", "rbf", "linear", "normal", "ar",...
algo = rpt.Binseg(model=model).fit(signal)
my_bkps = algo.predict(n_bkps=3)
# show results
rpt.show.display(signal, bkps, my_bkps, figsize=(10, 6))
plt.show()
# 변화점 개수를 모를 때
# my_bkps = algo.predict(pen=np.log(n) * dim * sigma**2)
# my_bkps = algo.predict(epsilon=3 * n * sigma**2)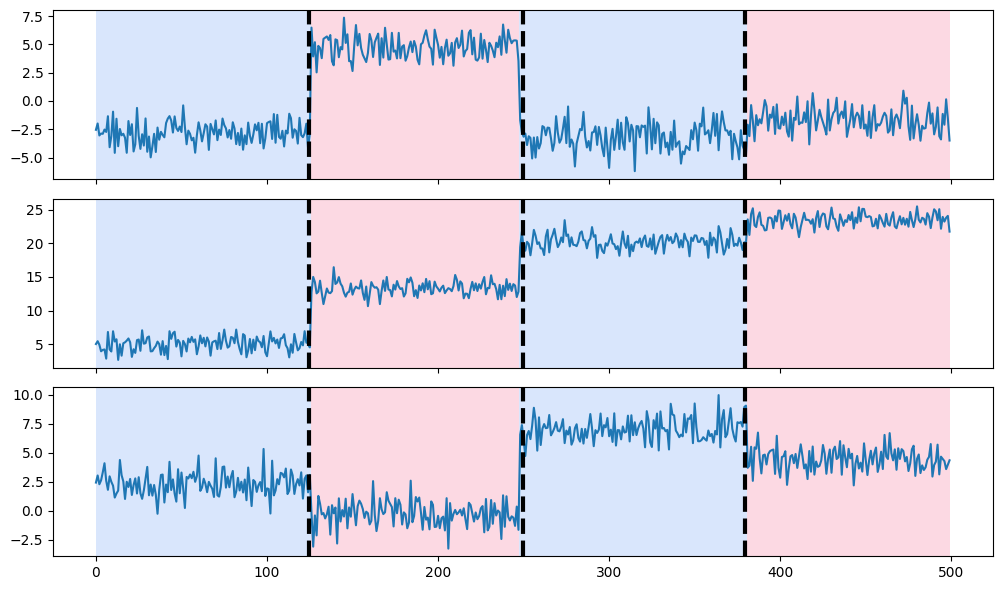
3) Bottom-up
모든 구간을 작은 단위로 나눈 후, 서로 비슷한 구간들을 합쳐 나가는 방식입니다. 변화점이 발생하지 않은 구간들을 차례로 합치면서 최종적으로 변화점이 있는 구간만 남깁니다. 변화점이 적은 데이터에서 유용하게 사용 가능하며 변화점 수를 알지 못해도 작동 가능합니다.

import numpy as np
import matplotlib.pylab as plt
import ruptures as rpt
# creation of data
n, dim = 500, 3 # number of samples, dimension
n_bkps, sigma = 3, 1 # number of change points, noise standart deviation
signal, bkps = rpt.pw_constant(n, dim, n_bkps, noise_std=sigma)
# change point detection
model = "l2" # "l1", "rbf", "linear", "normal", "ar"
algo = rpt.BottomUp(model=model).fit(signal)
my_bkps = algo.predict(n_bkps=3)
# show results
rpt.show.display(signal, bkps, my_bkps, figsize=(10, 6))
plt.show()
# 변화점 개수 알 수 없을 때
# my_bkps = algo.predict(pen=np.log(n) * dim * sigma**2)
# my_bkps = algo.predict(epsilon=3 * n * sigma**2)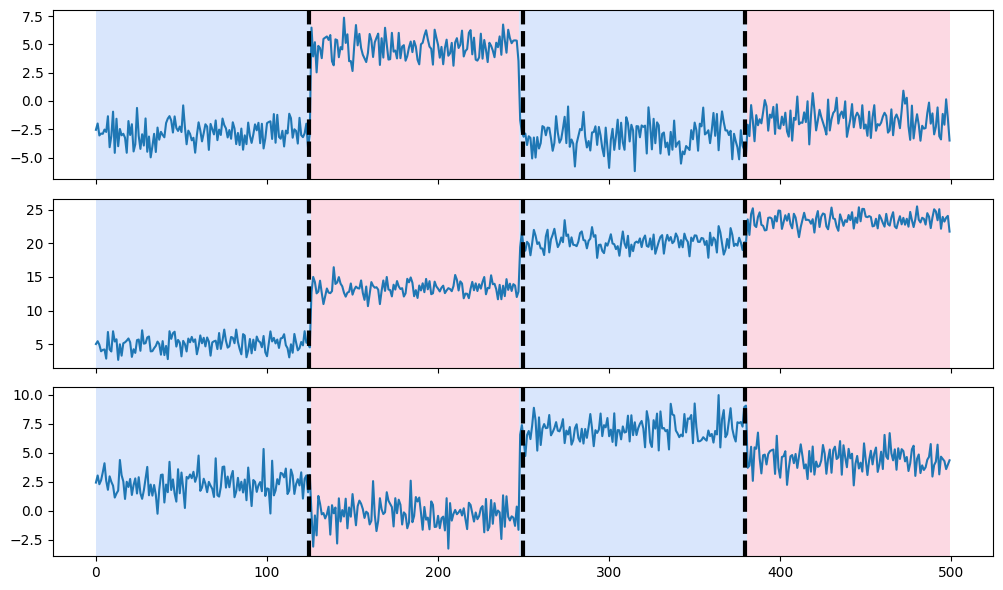
4) DP (Dynamic Programming)
최적의 변화점을 찾기 위해 동적 프로그래밍을 사용합니다. 주어진 신호의 모든 하위 시퀀스의 비용을 계산하여 비용 합의 정확한 최소값을 찾습니다. 모든 가능한 분할에 대한 검색이 동적 프로그래밍 접근 방식을 사용해 정렬됩니다. 변경점 개수를 미리 지정해야 하며 비용이 크지만 최적 해를 제공하기 때문에 정확한 변경점 탐지가 필요한 데이터에 적합합니다.
import numpy as np
import matplotlib.pylab as plt
import ruptures as rpt
# creation of data
n, dim = 500, 3
n_bkps, sigma = 3, 1
signal, bkps = rpt.pw_constant(n, dim, n_bkps, noise_std=sigma)
# change point detection
model = "l1" # "l2", "rbf"
algo = rpt.Dynp(model=model, min_size=3, jump=5).fit(signal)
my_bkps = algo.predict(n_bkps=3)
# show results
rpt.show.display(signal, bkps, my_bkps, figsize=(10, 6))
plt.show()

5) KernelCPD
데이터를 커널을 통해 고차원 공간으로 변환하여 매핑된 신호의 평균 변화로 변화를 탐지합니다. 커널 공간으로 변환하며 변화점 탐지의 민감도가 높아졌으며 비선형패턴에서의 변화도 잘 감지할 수 있습니다. 데이터의 특성에 따라 다양한 커널 함수(rbf, linear, cosine)를 선택해 사용 가능하고 단일 시그널 뿐 아니라 다변량 시그널에서도 변화점 탐지가 가능해 여러 변수가 동시에 변화할 때에도 효과적으로 탐지할 수 있다는 장점이 있습니다. 패널티로 민감도를 조절해 변화점의 개수를 조절할 수 있습니다.
import numpy as np
import matplotlib.pylab as plt
import ruptures as rpt
# creation of data
n, dim = 500, 3 # number of samples, dimension
n_bkps, sigma = 3, 1 # number of change points, noise standart deviation
signal, bkps = rpt.pw_constant(n, dim, n_bkps, noise_std=sigma)
# change point detection
kernel = "linear" # "rbf", "cosine"
algo = rpt.KernelCPD(kernel=kernel, min_size=2).fit(signal)
my_bkps = algo.predict(n_bkps=3)
# show results
rpt.show.display(signal, bkps, my_bkps, figsize=(10, 6))
plt.show()
# 변화점 개수 모를 때
# my_bkps = algo.predict(pen=10)
< Offline CPD 알고리즘 특징 요약 >
| 기준 | PELT | Binary Segmentation |
Bottom-up | Dynamic Programming (DP) |
KernelCPD |
| 변화점 탐지 방식 |
전체 신호를 분할하여 변화점의 최적 구간 탐색 | 신호를 반복적으로 분할해 점진적으로 변화점 탐지 | 초기 구간을 세분화하고 병합하며 변화점 탐지 | 최적 분할을 위해 전체 신호에서 동적 계획법 사용 | 커널 기반 비용함수를 이용해 비선형 데이터의 변화점 탐지 |
| 비용함수 | l1, l2, rbf | l1, l2, rbf, linear, normal, ar, | l1, l2, rbf, linear, normal, ar |
l1, l2, rbf | linear(l2), rbf, cosine |
| 탐지 정확도 | 높음 (노이즈에 강함) | 중간(과탐 위험) | 중간 (복잡한 패턴에 약함) |
매우 높음 (최적 해) | 매우 높음 (비선형 패턴) |
| 연산 효율성 | 매우 빠름 O(n) |
빠름 O(n lon n) |
빠름 O(n log n) |
매우 느림 O(n2) |
효율성 중간, 커널 종류에 따라 달라짐 |
| 변화점 수 조절 | 자동 조절 가능 변화점 수 고정 불가 |
자동 조절 가능 | 자동 조절 가능 | 변화점 수 고정 | 자동 조절 가능 |
| 다변량 가능 여부 |
가능 | 단일 시계열 | 단일 시계열 | 가능 | 가능 |
| 효과적 패턴 | 점진적 변화 | 급격한 변화 | 점진적 변화 | 복잡한 변화, 변화 빈도 잦은 패턴 |
비선형 패턴, 스파이크 패턴 |
| 활용 | 큰 규모의 시계열 데이터 | 비교적 간단한 시계열 데이터 | 변화점이 적은 데이터 | 정확한 탐지가 필요한 데이터 (의료 및 금융) | 비선형 데이터, 다변량 데이터 |
- PELT : 빠른 연산 속도와 높은 정확도를 제공하여 대규모 데이터에 적합한 알고리즘으로 자동으로 최적의 변화점을 찾아줌.
- Binary Segmentation : 빠르게 변화점을 찾지만 과탐지 위험이 있어 단순한 시계열 데이터에 효과적.
- Bottom-up Segmentation : 초기 세분화 후 병합하는 방식으로, 점진적 변화에 적합하나 복잡한 패턴에 약함.
- Dynamic Programming (DP): 최적의 정확도를 제공하지만 연산 속도가 느리기 때문에 정밀 탐지가 필요한 데이터에 유리.
- KernelCPD : 비선형 및 다변량 데이터에 효과적이며, 다양한 커널 선택과 패널티 조정으로 유연성이 큼.
3. 요약
- Change Point Detection은 시계열 데이터의 데이터 특성이 변화하는 지점을 찾는 기법이다.
- CPD는 크게 Online과 Offline 방식으로 나뉘며 실시간인지 과거 데이터 기반인지를 고려해 모델을 선택해야 한다.
- 마찬가지로, 데이터의 규모나 데이터의 특성과 패턴에 따라 알고리즘을 선택할 필요가 있다.
이번 글에서는 변화가 크게 나타나는 간단한 시계열 데이터를 만들어서 비교했지만 이후 글에서 비선형 패턴, 스파이크 패턴 등 다양한 패턴에서 각 알고리즘이 어떻게 변화점을 나타내는지 비교해보고, 비용함수가 실제로 어떻게 계산되어 변화점을 찾는지 추가로 소개해보도록 하겠습니다.
참고자료
- Centre Borelli. "ruptures: change point detection for Python." ruptures documentation.
- Truong, C., Oudre, L., & Vayatis, N. "Selective review of offline change point detection methods." Journal of Computational and Graphical Statistics, 2020.
'데이터분석' 카테고리의 다른 글
| [데이터시각화] 지수표현(+e)된 축 눈금 일반 숫자 형식으로 바꾸기 (0) | 2024.03.20 |
|---|---|
| [데이터시각화] 시계열 그래프 위에 결측정보 text로 겹치지 않게 표시하기 (0) | 2024.03.20 |
| [Python] 조건에 해당하는 array 값 변경 (0) | 2024.02.21 |
| [Python] min-max 벗어난 값을 min, max값으로 대체하기 (1) | 2024.02.21 |