Today's keyword : DFS, DP
📌 문제설명
https://www.acmicpc.net/problem/17070



📌 문제풀이
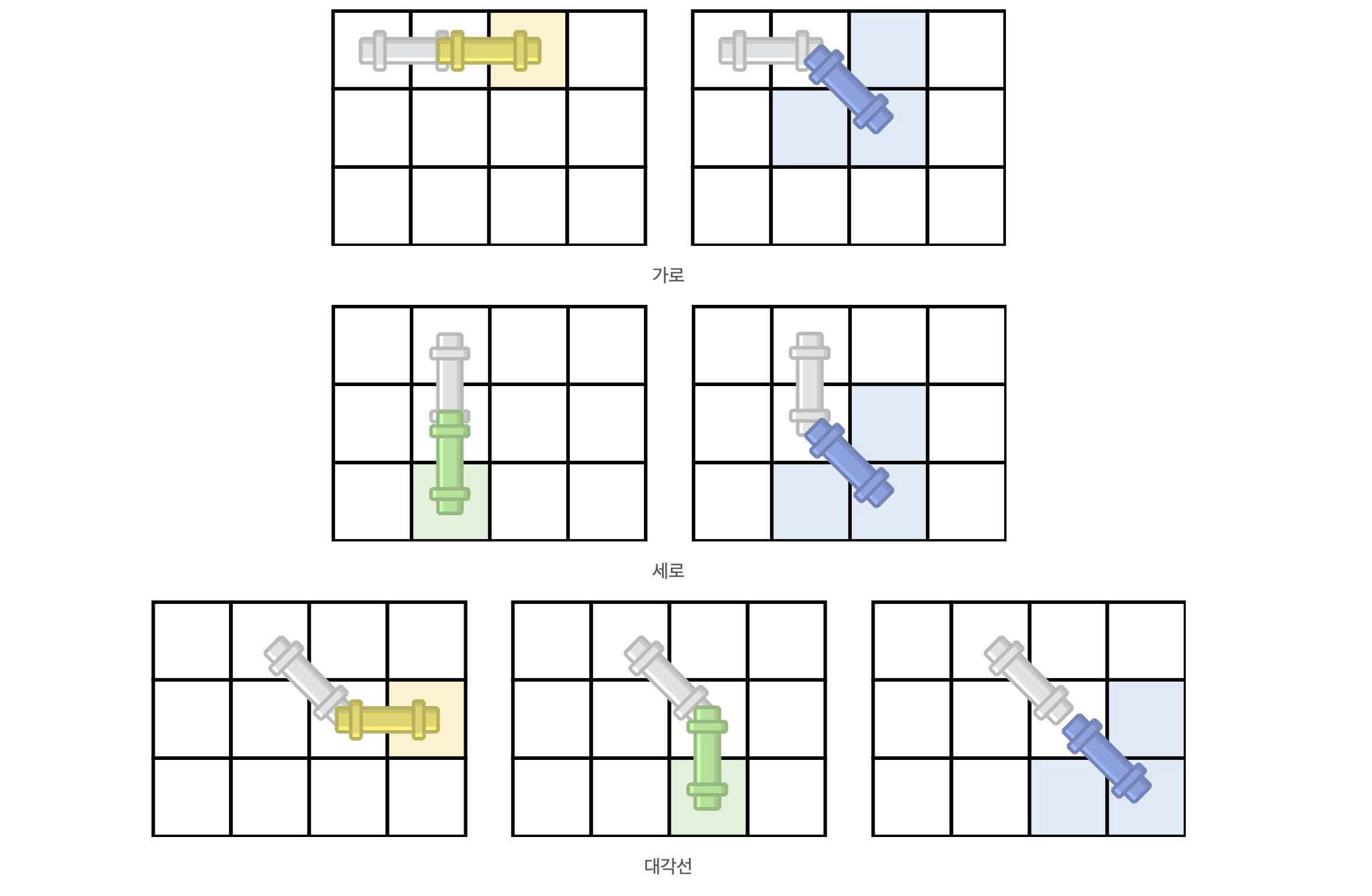
"파이프 옮기기" 문제는 N x N 격자에서 파이프를 이동시키는 문제입니다. 파이프는 수평, 수직, 대각선으로 놓일 수 있으며, 파이프의 시작 위치는 (0, 0)이고 목표 위치는 (N-1, N-1)입니다. 파이프는 장애물에 의해 이동할 수 없으며, 파이프가 목표 위치에 도달하는 모든 경우의 수를 구하는 것이 목표입니다.
풀이방법 1. 메모이제이션과 DFS
- DFS (Depth-First Search): 재귀적으로 가능한 모든 경로를 탐색하는 방법입니다. 각 위치에서 이동 가능한 모든 방향으로 이동하며, 목표 위치에 도달할 때마다 경우의 수를 증가시킵니다.
- 메모이제이션: 이미 계산한 결과를 저장하여 중복 계산을 피하는 기법입니다. 각 상태 (x, y, direction)에 대한 경우의 수를 저장하여, 같은 상태에 도달했을 때는 저장된 값을 반환합니다.
import sys
input = sys.stdin.readline # 빠른 입력을 위해 sys.stdin.readline 사용
sys.setrecursionlimit(1_000_000) # 재귀 호출의 최대 깊이를 설정
n = int(input()) # 격자의 크기 N을 입력받음
graph = [] # 격자 정보를 저장할 리스트
# 격자 정보를 입력받아 graph에 저장
for i in range(n):
graph.append(list(map(int, input().split())))
# 메모이제이션을 위한 배열: (x, y, direction)
# memo[x][y][direction]은 (x, y) 위치에서 direction 방향으로 놓인 파이프의 경우의 수를 저장
memo = [[[-1] * 3 for _ in range(n)] for _ in range(n)]
def move_pipe(x, y, direction, grid, N):
# 기저 조건: 파이프가 목표 위치에 도달했을 때
if x == N - 1 and y == N - 1:
return 1 # 경우의 수 1 증가
# 이미 계산된 경우의 수가 있다면 반환
if memo[x][y][direction] != -1:
return memo[x][y][direction]
count = 0 # 경우의 수 초기화
# 현재 방향에 따라 다음 위치로 이동
if direction == 0: # 수평
# 수평으로 이동
if y + 1 < N and grid[x][y + 1] == 0: # 오른쪽으로 이동 가능
count += move_pipe(x, y + 1, 0, grid, N) # 수평 유지
# 대각선으로 이동
if x + 1 < N and y + 1 < N and grid[x + 1][y + 1] == 0 and grid[x][y + 1] == 0 and grid[x + 1][y] == 0:
count += move_pipe(x + 1, y + 1, 2, grid, N) # 대각선으로 이동
elif direction == 1: # 수직
# 수직으로 이동
if x + 1 < N and grid[x + 1][y] == 0: # 아래로 이동 가능
count += move_pipe(x + 1, y, 1, grid, N) # 수직 유지
# 대각선으로 이동
if x + 1 < N and y + 1 < N and grid[x + 1][y + 1] == 0 and grid[x][y + 1] == 0 and grid[x + 1][y] == 0:
count += move_pipe(x + 1, y + 1, 2, grid, N) # 대각선으로 이동
elif direction == 2: # 대각선
# 수평으로 이동
if y + 1 < N and grid[x][y + 1] == 0: # 오른쪽으로 이동 가능
count += move_pipe(x, y + 1, 0, grid, N) # 수평으로 이동
# 수직으로 이동
if x + 1 < N and grid[x + 1][y] == 0: # 아래로 이동 가능
count += move_pipe(x + 1, y, 1, grid, N) # 수직으로 이동
# 대각선으로 이동
if x + 1 < N and y + 1 < N and grid[x + 1][y + 1] == 0 and grid[x][y + 1] == 0 and grid[x + 1][y] == 0:
count += move_pipe(x + 1, y + 1, 2, grid, N) # 대각선으로 이동
# 계산한 경우의 수를 메모이제이션 배열에 저장
memo[x][y][direction] = count
return count # 경우의 수 반환
# 초기 위치 (0, 1)에서 수평 방향으로 시작하여 경우의 수를 계산
print(move_pipe(0, 1, 0, graph, n))- 입력 처리: N x N 격자의 크기 n와 장애물 정보 grid를 입력받습니다.
- 재귀 함수 정의: move_pipe(x, y, direction) 함수를 정의하여 현재 위치와 방향을 인자로 받습니다.
- 기저 조건: 현재 위치가 목표 위치 (N-1, N-1) 에 도달했을 때 경우의 수를 1 증가시킵니다.
- 이동 가능성 체크: 현재 방향에 따라 이동할 수 있는지 확인하고, 유효한 경우에만 재귀 호출을 진행합니다.
- 메모이제이션: 각 상태에 대한 경우의 수를 저장하여 중복 계산을 방지합니다.
풀이방법 2. DP
- 상태 정의: DP를 사용할 때는 각 상태를 정의하고, 이전 상태의 결과를 이용하여 현재 상태의 결과를 계산합니다. 이 문제에서는 dp[x][y][direction] 배열을 사용하여 각 위치와 방향에 대한 경우의 수를 저장합니다.
- 점화식: 각 방향에 따라 이동할 수 있는 경우의 수를 점화식으로 정의합니다. 예를 들어, 수평 방향에서 오른쪽으로 이동할 수 있는 경우와 대각선으로 이동할 수 있는 경우를 고려합니다.
- 하향식 접근: DP는 보통 하향식 접근을 사용하여 작은 문제부터 해결해 나가며, 최종적으로 큰 문제를 해결합니다.
n = int(input())
grid = [list(map(int, input().split())) for _ in range(n)]
# dp[x][y][direction]: (x, y) 위치에서 direction 방향으로 놓인 파이프의 경우의 수
dp = [[[0] * 3 for _ in range(n)] for _ in range(n)]
# 초기 상태: (0, 1) 위치에 수평으로 놓인 파이프
dp[0][1][0] = 1
for x in range(n):
for y in range(n):
# 수평 방향
if y + 1 < n and grid[x][y + 1] == 0: # 오른쪽으로 이동 가능
dp[x][y + 1][0] += dp[x][y][0] # 수평 유지
if x + 1 < n and y + 1 < n and grid[x + 1][y + 1] == 0 and grid[x][y + 1] == 0 and grid[x + 1][y] == 0:
dp[x + 1][y + 1][2] += dp[x][y][0] # 대각선으로 이동
# 수직 방향
if x + 1 < n and grid[x + 1][y] == 0: # 아래로 이동 가능
dp[x + 1][y][1] += dp[x][y][1] # 수직 유지
if x + 1 < n and y + 1 < n and grid[x + 1][y + 1] == 0 and grid[x][y + 1] == 0 and grid[x + 1][y] == 0:
dp[x + 1][y + 1][2] += dp[x][y][1] # 대각선으로 이동
# 대각선 방향
if y + 1 < n and grid[x][y + 1] == 0: # 오른쪽으로 이동 가능
dp[x][y + 1][0] += dp[x][y][2] # 수평으로 이동
if x + 1 < n and grid[x + 1][y] == 0: # 아래로 이동 가능
dp[x + 1][y][1] += dp[x][y][2] # 수직으로 이동
if x + 1 < n and y + 1 < n and grid[x + 1][y + 1] == 0 and grid[x][y + 1] == 0 and grid[x + 1][y] == 0:
dp[x + 1][y + 1][2] += dp[x][y][2] # 대각선으로 이동
# 결과 출력: (N-1, N-1) 위치에 도달하는 경우의 수
result = dp[n - 1][n - 1][0] + dp[n - 1][n - 1][1] + dp[n - 1][n - 1][2]
print(result)- 입력 처리:
- n을 입력받아 격자의 크기를 결정합니다.
- grid 리스트를 사용하여 N x N 격자의 장애물 정보를 입력받습니다. 장애물은 1로 표시되고, 빈 공간은 0으로 표시됩니다.
- DP 테이블 초기화:
- dp 배열을 3차원으로 초기화합니다. dp[x][y][direction]은 (x, y) 위치에서 direction 방향으로 놓인 파이프의 경우의 수를 저장합니다.
- direction은 0(수평), 1(수직), 2(대각선)으로 정의됩니다.
- 초기 상태 설정:
- 파이프가 (0, 1) 위치에 수평으로 놓여 있으므로, dp[0][1][0]을 1로 설정합니다. 이는 파이프가 시작 위치에 있을 때의 경우의 수입니다.
- DP 테이블 채우기:
- 이중 루프를 사용하여 격자의 모든 위치 (x, y)를 순회합니다.
- 각 방향에 따라 이동할 수 있는 경우를 체크하고, 가능한 경우의 수를 업데이트합니다.
- 수평 방향: 오른쪽으로 이동할 수 있는 경우와 대각선으로 이동할 수 있는 경우를 체크합니다.
- 수직 방향: 아래로 이동할 수 있는 경우와 대각선으로 이동할 수 있는 경우를 체크합니다.
- 대각선 방향: 오른쪽으로, 아래로, 대각선으로 이동할 수 있는 경우를 체크합니다.
- 결과 계산:
- 최종적으로 (N-1, N-1) 위치에 도달하는 경우의 수를 계산합니다. 이는 수평, 수직, 대각선 방향으로 놓인 파이프의 경우의 수를 모두 더하여 결과를 출력합니다.
📌 오늘의 회고
아직 DP 방식은 익숙하지 않다. DFS에서도 메모이제이션을 쓰지 않으면 시간초과가 나므로 주의해야 한다.
'Algorithm' 카테고리의 다른 글
| [TIL] 99클럽 코테 스터디 15일차 TIL - 그리디: <백준 13417 카드문자열>문제 풀이 with python (2) | 2024.11.12 |
|---|---|
| [TIL] 99클럽 코테 스터디 14일차 TIL - 그리디 : <백준 14916 거스름돈> 문제 풀이 with python (1) | 2024.11.10 |
| <백준 13335 : 트럭> 문제풀이 with python (5) | 2024.11.09 |
| [TIL] 99클럽 코테 스터디 13일차 TIL - 이진탐색 : 백준 10561 징검다리 문제 풀이 with python (1) | 2024.11.09 |
| [TIL] 99클럽 코테 스터디 7일차 TIL - <프로그래머스 : 10561 징검다리> 문제 풀이 with python (2) | 2024.11.04 |