목차
1. 개념 및 용어
2. 알고리즘 동작원리
3. 배낭문제 Python 구현 코드
회사에서 최적화 관련 프로젝트를 진행하게 되면서 유전 알고리즘을 접하게 되어 유전 알고리즘이 어떤 것인지, 어떻게 최적화를 진행하는 것인지 배낭문제를 예시로 들어 정리해 보도록 하겠습니다.
1. 개념 및 용어
유전 알고리즘이란 생물체가 환경에 적응하며 진화하는 것처럼 가장 적합한 개체들이 선택되며 최적의 해를 찾는 알고리즘을 말합니다. 찰스 다윈의 자연선택 이론*에 영감을 얻어 존 홀랜드에 의해 1975년 개발되었습니다. 생물의 진화를 모방하였기 때문에 유전자와 염색체와 같은 개념과 실제 진화 과정인 교배 연산, 돌연변이의 개념을 그대로 차용하여 알고리즘 작동 원리에 녹아 있습니다.
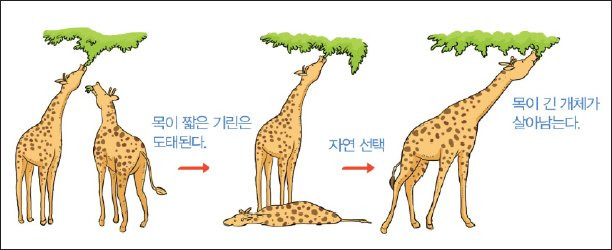
* 자연선택 이론 : 생존에 적합한 형질(키, 보조개 여부 등)을 지닌 개체군이 부적합한 형질을 지닌 개체군에 비해 ‘생존’과 ‘번식’에 이득을 본다는 이론
생물의 유전자가 세대를 거듭하면서 부와 모의 형질이 계속 섞이며 진화를 하는 것처럼, 유전 알고리즘도 부모의 유전자를 물려 받아 부의 데이터와 모의 데이터가 교차와 변이 되어 자손 데이터가 만들어지고, 자손들의 데이터들 중 적합한 자손들만 남아 세대를 계속 거듭해 나가며 최적화가 이루어집니다.
결국, 유전알고리즘은 풀고자 하는 문제의 최적화된 해를 찾기 위해 진화 과정을 모방해 만든 탐색 알고리즘이라고 말할 수 있습니다. 풀고자 하는 문제에 대해 가능한 해를 나타내고, 해당 해들이 세대를 거듭하며 점차 변형되며 좋은 해를 만들어내는 과정을 거쳐 최적화가 되거나 특정 세대를 만족하는 등 특정 종료 조건에 도달하게 되면 최종 해를 산출하게 됩니다.
용어
유전알고리즘에서는 생물 진화론에서 사용하고 있는 용어와 그 개념을 그대로 사용하고 있기에 좀 더 이해를 돕고자 진화론에서 사용하고 있는 의미와 유전알고리즘에서 사용되는 의미를 비교해보았습니다.
| 진화론 | 유전 알고리즘 | |
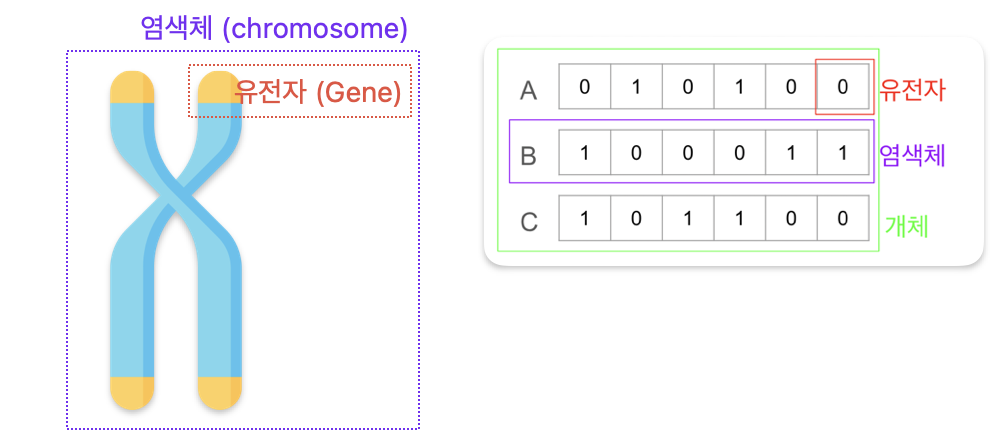
| 염색체 (Chromosome) |
생물의 세포 핵 내에 존재하는 DNA와 단백질의 복합체로, 유전 정보를 담고 있는 구조체 | 최적화하고자 하는 문제의 해답을 인코딩한 데이터 구조. 보통 이진수 문자열이나 실수, 정수의 배열 형태로 표현됨 |
| 유전자 (Gene) |
특정 형질을 결정하는 DNA의 특정 부분으로, 단백질 합성 등 생물학적 기능을 담당하는 유전 정보의 단위 | 염색체를 구성하는 하나의 단위 요소. 문제 해결을 위한 변수나 파라미터의 한 자리를 나타냄 |
| 개체 (Individual) |
한 생물종에 속하는 하나의 생명체 | 하나의 후보해(candidate solution)를 의미하며, 하나의 염색체로 표현됨 |
| 세대 (Generation) |
부모 세대로부터 자손이 태어나 다시 번식 가능한 시기가 될 때까지의 기간 | 한 번의 선택, 교차, 돌연변이 연산을 거쳐 새로운 개체들이 생성되는 한 주기 |
| 모집단 (Population) |
같은 종에 속하며 같은 지역에서 서로 교배 가능한 개체들의 집합 | 현재 세대에서 다루고 있는 후보해(염색체)들의 집합 |
| 적응도 (Fitness) |
특정 환경에서 생존하고 번식할 수 있는 능력을 나타내는 척도 | 각 후보해가 문제 해결에 얼마나 적합한지를 수치화한 값. 적합도 함수(Fitness function)의 값으로 계산됨 |
| 돌연변이 (Mutation) |
DNA 복제 과정에서 발생하는 우연한 변화로, 새로운 형질의 출현 원인 | 염색체의 특정 위치의 값을 임의로 변경하는 연산. 해 공간의 탐색 다양성을 확보하는 역할 |
| 교차 (Crossover) |
생식 과정에서 부모의 염색체가 교환되어 자손의 새로운 유전자 조합이 만들어지는 현상 | 두 개의 부모 해로부터 이들의 특징을 조합하여 새로운 자식 해를 만드는 연산 |
2. 알고리즘 주요 과정

유전 알고리즘이 동작되는 과정은 위에서 설명한 자연선택이론처럼 부모의 유전자를 물려받은 여러 자손 중 뛰어난, 적합도가 우수한 자손들만 번식을 계속하며 조건을 만족하는 최적의 자손을 찾을 때까지 세대를 거듭해 자손을 번식하며 탐색을 계속 진행하게 됩니다. 우수한 자손에 대한 평가를 위해 적합도를 계산하게 되고, 부모가 될 자손을 선택하기 위해 여러 선택 기법을 이용해 부모를 선택합니다. 부와 모의 유전자를 받기 위해 교차 연산을 진행하며, 다양성을 보장하기 위해 돌연변이 연산을 진행하게 됩니다. 세부적인 과정을 바로 아래에 구체적으로 설명드리겠습니다.
0. 솔루션 공간 인코딩
염색체를 구성할 때 어떤 데이터 타입으로 염색체를 구성할지를 설정하는 단계로, 데이터의 특성과 문제를 고려해 설정해야 합니다. 배낭문제에서 물건을 담는 지와 같이 간단한 문제의 경우에는 이진수로 표현 가능하지만 문제가 복잡해질수록 솔루션 공간에 인코딩하는 데이터도 복잡해지게 됩니다.
1. Binary Encoding (이진인코딩) : 0 혹은 1로 구성된 비트 문자열
- 예) 0101 … 0000
- 각각의 물건들의 무게와 가치는 다음과 같고, 배낭에 담을 수 있는 한계가 10kg일 때, 배낭에 담는 물건의 가치를 최대화하는 문제를 풀고 있다면, 다음과 같이 각 염색체는 이진 인코딩으로 표현할 수 있습니다.
| 무게 | 가치 | |
| 금화 | 7 | 7 |
| 검 | 6 | 4 |
| 도끼 | 5 | 3 |
| 반지 | 2 | 6 |
| 왕관 | 4 | 5 |
| 목걸이 | 3 | 5 |
| 염색체 | 금화 | 검 | 도끼 | 반지 | 왕관 | 목걸이 | 무게 (조건) | 가치 (=적합도) |
| A | 1 | 0 | 0 | 0 | 0 | 1 | 10kg | 12 |
| B | 0 | 0 | 0 | 1 | 1 | 1 | 9kg | 16 |
| ... | ... |
2. 실숫값 인코딩
- 예) 2.2, 3.7, -2.1 ...
- 위와 똑같은 배낭 문제에서 각 항목의 수량이 추가되었을 때는 각 항목의 수량을 인코딩하여 아래와 같이 염색체를 표현할 수 있습니다.
| 무게 | 가치 | 수량 | |
| 금화 | 7 | 7 | 1 |
| 검 | 6 | 4 | 2 |
| 도끼 | 5 | 3 | 3 |
| 반지 | 2 | 6 | 4 |
| 왕관 | 4 | 5 | 2 |
| 목걸이 | 3 | 5 | 4 |
| 금화 | 검 | 도끼 | 반지 | 왕관 | 목걸이 | 무게 | 가치 | |
| A | 0 | 0 | 0 | 0 | 1 | 2 | 10kg | 15 |
| B | 0 | 0 | 0 | 3 | 1 | 0 | 10kg | 23 |
| ... | ... |
3. 순서 인코딩
- 예) 3, 1, 4, 2
- 순서나 순열이 중요한 최적화 문제에 주로 사용됩니다. 예를 들어, 외판원 문제(TSP) 문제에서 도시들의 방문 순서를 나타낼 때 활용되거나 작업 스케쥴링에서 작업의 실행 순서를 나타낼 때 활용됩니다. 순서를 나타내기 때문에 각 유전자(숫자)는 염색체 내에서 한 번씩만 나타나야 합니다.
1. 초기 모집단 생성 (Initialize population)
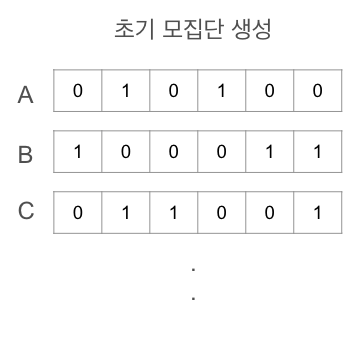
초기 모집단 생성은 자손을 번식할 최초의 부모, 조상을 생성하는 단계입니다. 임의의 값들로 염색체를 구성합니다.
위에 배낭문제를 예시로 들면, 배낭에 들어가는 물건들의 개수를 랜덤하게 가진 염색체를 N개만큼 설정하게 됩니다. 임의의 값으로 설정되기 때문에 어떤 염색체는 검만 3개 가질 수도 있고, 어떤 염색체는 모든 물건들을 1개씩 가질 수도 있습니다.
2. 개체의 적합도 측정

어떤 염색체가 생존에 유리한 지 측정하는 단계로, 설정한 적합도 함수에 의해 각 염색체의 적합도가 측정됩니다.
배낭문제에서의 적합도는 물건들의 가치로 계산될 수 있으며, 설정된 물건들의 개수에 맞춰 가치를 계산하게 됩니다.
3. 적합도에 따른 부모 선택 (Selection)

생존에 적합한 개체가 살아남아 자손을 번식하는 것처럼 생존에 적합한 개체를 추리는 단계로, 다음 세대에 유전 정보를 전달할 부모를 선택하는 과정입니다. 이전에 측정한 적합도를 바탕으로 특정 기준을 충족하는 부모만 선택되게 됩니다. 부모를 선택할 때에는 적합도가 높은 순으로 선택하는 것이 아니라 확률적으로 선택하게 됩니다. 적합도가 높을수록 부모가 될 확률이 높아진다는 의미로, 위 예시처럼 적합도가 가장 높은 C와 D가 선택되지 않고, 적합도가 비교적 낮은 염색체가 부모로 선택될 수도 있습니다. 또한, 선택 과정이 확률적으로 결정되기 때문에 유전알고리즘은 항상 같은 결과를 보장하진 않습니다.
염색체를 선택하는 방법은 룰렛 휠, 볼츠만(Boltzman), 토너먼트, 순위 선택, steady selection 등 여러 방법이 존재하며 그중 주요 방법인 룰렛 휠과 순위 선택, 토너먼트 선택, 엘리트주의 선택에 대해 설명드리겠습니다.
1) 룰렛 휠 (Roulette wheel Selection)
적합도에 비례하여 부모를 선택하는 방법으로, 적합도에 비례하는 만큼 휠 부분의 크기가 할당되어 적합도가 높을수록 부모에 선택될 확률이 커지게 됩니다. 아래 그림처럼 각 염색체의 적합도가 10, 30, 40, 20, 10으로 나타났을 때, 해당 염색체가 부모로 선택될 확률은 각 적합도에 비례하여 계산됩니다. C 염색체가 가장 큰 적합도인 40을 가지고 있기 때문에 부모로 선택될 확률이 36%로 가장 크며, 가장 낮은 적합도를 가진 A와 E는 부모로 선택될 확률이 9%씩 존재합니다.

2) 순위 선택(Rank Selection)
룰렛 휠 방법은 적합도 크기 차이가 매우 크거나 차이가 없을 때 문제가 발생할 수 있습니다. 최고의 염색체의 적합도가 90%를 차지하면 나머지 염색체는 선택될 가능성이 거의 없어지게 되기 때문입니다. 반대로 차이가 미미할 때 실적이 저조한 개체에 더 많은 선택에 기회를 주게 되어 다양성이 증가하여 최적 솔루션을 찾는 데 더 오랜 시간이 필요할 수도 있습니다. 순위 선택 방법은 이런 한계를 극복하기 위해 적합도 값 자체가 아닌 적합도의 순위에 비례하여 부모를 선택하는 기법입니다.
적합도 크기 차이가 큰 경우일 때 룰렛 휠 선택 방법과 순위 선택 방법을 비교해 보면, 룰렛 휠 방법에 의하면 E가 선택될 확률은 1%로 매우 작게 나타나지만, 순위 선택 방법에 의하면 7%로 나타납니다. 적합도가 높은 염색체만 선택되게끔 한다면 룰렛 휠 선택 방법이 괜찮지만, 다양성을 유지한 채 최대한 탐색 범위를 넓히고 싶다면 순위 선택 방법이 적절해 보입니다.

3) 토너먼트 선택 (Tournament Selection)
정해진 수의 개체를 무작위로 그룹에 배치하고 각 그룹 안에서 적합도 점수가 가장 높은 개체를 선택하는 방법입니다. 각 그룹에서 한 개의 개체만 선택되므로 그룹이 클수록 다양성이 떨어지게 됩니다. 토너먼트의 규모로 선택의 강도를 조절할 수 있으며, 강한 적합도만 선택하려면 토너먼트 사이즈를 키우면 되고, 작은 토너먼트를 만들면 약한 개체들이 선택될 확률이 증가하여 다양성이 증가됩니다.
4) 엘리트주의 선택
적합도가 가장 높은 일부 개체를 무조건 다음 세대로 전달하는 방법으로, 모집단이 지역 최고 솔루션 공간에 빠져 전역 최고 솔루션을 찾을 만큼 다양해질 수 없을 수가 있다는 단점이 존재합니다. 최고라고 생각한 염색체만 다음 세대에 전달했지만, 알고 보니 일부분에서는 최고의 염색체라도 전체로 봤을 때는 최고의 염색체가 아니었기에 최종적으로 다양하게 탐색하지 못하고 최적해를 못 찾을 수가 있게 됩니다. 그래서 종종 엘리트주의 선택만 사용하는 것이 아니라 룰렛 휠 선택, 토너먼트 선택과 함께 사용되어 엘리트 개체 선택 후 나머지 모집단에서 다른 전략을 사용하여 다양성을 보장합니다.
4. 자손 번식 : 유전 연산을 통해 자손 생성
1) 교차 (Crossover) : 부와 모의 유전 정보를 결합해 자손 생성

자식이 엄마의 눈을 닮고, 아빠의 코를 닮는 것처럼 유전 알고리즘에서도 부의 염색체와 모의 염색체에서 각각 어떤 정보를 담은 유전자가 섞여 자손을 생성하게 됩니다.
부와 모의 유전자를 어떻게 나눠 결합하느냐에 따라 단일 지점 교배, 다중 지점 교배, 균등 교배, 산술 교차로 구분되며, 문제의 특성과 인코딩 방식, 계산 복잡도를 고려하여 방법을 선택해야 합니다.
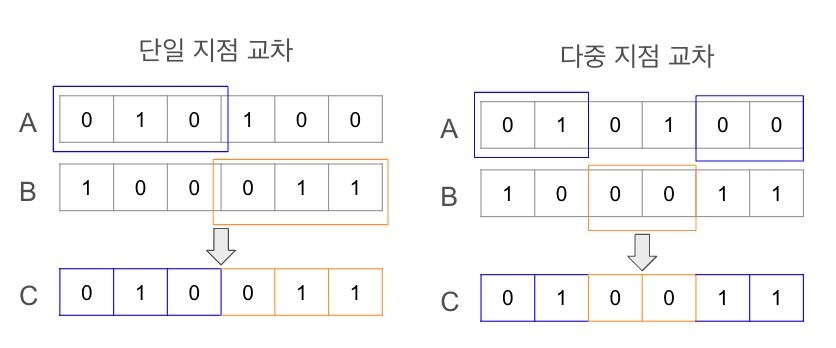
- 단일 지점 교차 (Single Point Crossover): 한 지점을 기준으로 부모의 유전자를 교환하는 방식으로 위 그림의 예시처럼 가운데를 기준으로 A에서는 왼쪽에 위치한 유전자를 물려받고, B에서는 오른쪽에 위치한 유전자를 물려받아 자손 C가 생성됩니다.
- 다중 지점 교차 (Multi-Point Crossover): 여러 지점에서 유전자를 교환하는 방식입니다.
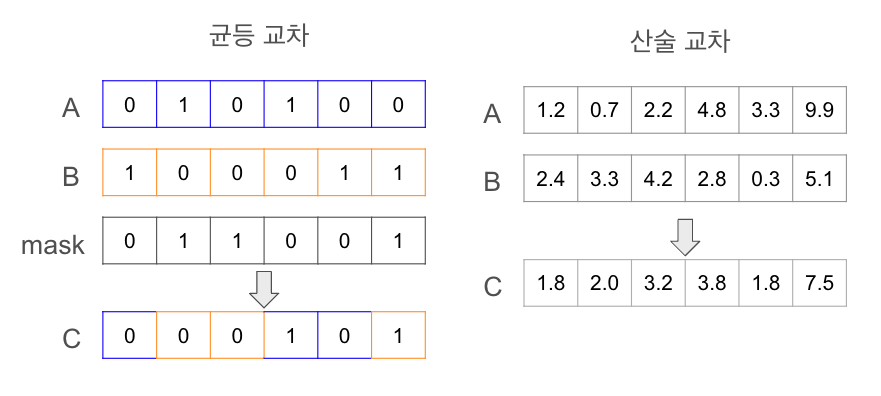
- 균등 교차 (Uniform Crossover): 각 유전자를 랜덤 하게 부모 중 한쪽에서 선택하는 방식입니다. 랜덤하게 마스크를 구성한 후, 어느 쪽의 유전자를 받아들일지 결정합니다. A라는 염색체를 받는다고 한다면, 마스크에서 0인 유전자는 그대로 전달하고, 1일 때는 B의 유전자를 받아 자손을 생성합니다.
- 산술 교차(Arithmetic Crossover) : 실수 표현을 사용할 때 사용하며, 두 부모 염색체 유전자의 평균값 등 산술식을 이용해 자손을 생성하는 방법으로, 다양한 자손을 생성하기 때문에 주의가 필요합니다.
2) 돌연변이 : 일정 확률로 개체의 유전자를 변경해 탐색 공간의 다양성을 유지
유전 알고리즘에서 돌연변이는 알고리즘의 다양성을 유지하고, 지역 최적해에 빠지는 것을 방지해 주는 역할을 합니다. 특정 확률(0.1, 0.05와 같이 낮은 확률)을 설정한 후, 해당 비율만큼 돌연변이 연산에 의해 돌연변이 자손을 생성하게 됩니다.
돌연변이의 주요 방법들은 다음과 같습니다.

- 비트 플립 변이(Bit Flip Mutation) : 이진 표현에서 무작위로 선택된 비트의 값을 반전시킵니다.
- 랜덤 리셋팅 변이(Random Resetting Mutation): 선택된 유전자의 값을 무작위로 변경합니다
- 스왑 변이(Swap Mutation): 두 개의 유전자 위치를 무작위로 선택하여 그 값을 교환합니다.
- 스크램블 변이(Scramble Mutation): 선택된 부분 문자열 내의 유전자 순서를 무작위로 섞습니다.
- 역전 변이(Inversion Mutation): 선택된 부분 문자열의 순서를 뒤집습니다
이외에도 실수 인코딩의 경우, 현재 값에 정규분포 노이즈를 추가하여 돌연변이를 생성하는 가우시안 돌연변이 방법 외에도 무작위로 선택한 유전자에 작은 수를 더하거나 빼 돌연변이를 생성하거나 특정 범위(min, max) 내에서 무작위 값으로 변경하는 등 여러 돌연변이 연산을 사용할 수 있습니다.
5. 종료 조건 (Termination Criteria)
알고리즘을 멈출 조건을 설정하여 조건 만족 시 최적해를 도출하게 됩니다. 종료 조건 예시로는 지정한 최대 세대수에 도달하거나 특정 적합도 이상 도달하거나 적합도 개선이 일정 기간 없을 때 등이 있습니다.
3. 배낭문제 Python 구현 코드
위에서 유전 알고리즘의 기본 개념과 동작원리를 살펴보았는데, 동작원리를 보다 이해할 수 있도록 배낭문제를 예시로 파이썬으로 간단하게 구현해 보겠습니다.
여기서는 배낭의 최대 무게가 15kg이며, 배낭 안에 넣을 수 있는 물건은 금화, 검, 도끼, 반지, 왕관, 목걸이가 있습니다. 각각의 물건은 한 개씩 존재하며 각 물건의 가치는 아래 표와 같습니다. 세대수는 최대 50 세대로 설정하고, 돌연변이 확률은 0.1로 설정하였습니다.
| 무게 | 가치 | |
| 금화 | 7 | 7 |
| 검 | 6 | 4 |
| 도끼 | 5 | 3 |
| 반지 | 2 | 6 |
| 왕관 | 4 | 5 |
| 목걸이 | 3 | 5 |
import random
# 배낭 문제 데이터
items = [
{"name": "금화", "weight": 7, "value": 7},
{"name": "검", "weight": 6, "value": 4},
{"name": "도끼", "weight": 5, "value": 3},
{"name": "반지", "weight": 2, "value": 6},
{"name": "왕관", "weight": 4, "value": 5},
{"name": "목걸이", "weight": 3, "value": 5},
]
max_weight = 15 # 배낭의 최대 무게 제한
population_size = 10 # 초기 개체군 크기
generations = 50 # 세대 수
mutation_rate = 0.1 # 돌연변이 확률
# 적합도 함수: 선택된 아이템의 총 가치 반환
def fitness(individual):
total_weight = sum(ind * item["weight"] for ind, item in zip(individual, items))
total_value = sum(ind * item["value"] for ind, item in zip(individual, items))
if total_weight > max_weight: # 무게 초과 시 적합도 0
return 0
return total_value
# 초기 개체군 생성
def initialize_population():
return [[random.randint(0, 1) for _ in range(len(items))] for _ in range(population_size)]
# 선택 (룰렛 휠 선택)
def select_parents(population):
fitness_values = [fitness(ind) for ind in population]
total_fitness = sum(fitness_values)
if total_fitness == 0: # 모든 적합도가 0인 경우 랜덤 선택
return random.sample(population, 2)
probabilities = [f / total_fitness for f in fitness_values]
return random.choices(population, probabilities, k=2)
# 교배 (단일 지점 교배)
def crossover(parent1, parent2):
point = random.randint(1, len(items) - 1)
child1 = parent1[:point] + parent2[point:]
child2 = parent2[:point] + parent1[point:]
return child1, child2
# 돌연변이
def mutate(individual):
for i in range(len(individual)):
if random.random() < mutation_rate:
individual[i] = 1 - individual[i] # 0을 1로, 1을 0으로 뒤집음
# 유전 알고리즘 실행
def genetic_algorithm():
population = initialize_population()
for generation in range(generations):
# 다음 세대 생성
new_population = []
for _ in range(population_size // 2):
parent1, parent2 = select_parents(population)
child1, child2 = crossover(parent1, parent2)
mutate(child1)
mutate(child2)
new_population.extend([child1, child2])
population = new_population
# 현재 세대의 최적해 출력
best_individual = max(population, key=fitness)
print(f"세대 {generation + 1}: 최적 가치 = {fitness(best_individual)}, 선택 = {best_individual}")
# 최종 결과
best_individual = max(population, key=fitness)
print("\\n최적해:")
print(f"선택된 아이템: {[items[i]['name'] for i in range(len(items)) if best_individual[i] == 1]}")
print(f"최종 가치: {fitness(best_individual)}")
# 실행
genetic_algorithm()
유전 알고리즘의 동작 원리에서 살펴본 것처럼 주요 과정을 함수로 만들고, 초기 염색체를 생성 후, 교차와 변이를 진행하며 최대 세대 수가 도달할 때까지 자손을 번식시켜 보았습니다. 결과는 아래와 같이 금화, 반지 왕관을 배낭에 넣었을 때가 최적이며 18이라는 가치를 가진다고 나왔습니다.

하지만 세 번째 돌렸을 때 결과는 '금화', '검', '반지'로 나타났으며, 이때 최종 가치는 17이었습니다.

유전 알고리즘은 다양한 유형의 복잡한 문제에 적용 가능한 유용한 최적화 도구이지만, 위와 같이 항상 최적해를 찾는다는 보장이 없고 모집단 크기, 돌연변이 비율 등 파라미터 조정이 필요하며, 큰 집단 크기나 복잡한 적합도 함수일 경우 계산 비용이 높아 수렴 속도가 느릴 수 있습니다. 그럼에도 현실에 적용하는 최적화 문제에서는 여러 제약조건들을 고려해 복잡한 문제를 해결하기 위해 유전 알고리즘을 여전히 강력한 도구로 사용하고 있습니다.
+) 추가 유의사항 : 순위 선택 시 무게 제한을 만족하는 개체만 필터링하기
정말 마지막으로, 순위 선택 방법으로 부모를 선택할 때 경험했던 오류 상황에 대해 간단하게 언급하며 마무리하겠습니다.
룰렛 휠의 경우 무게가 제한을 넘는 개체는 적합도가 0으로 계산되어 부모 선택 확률도 0이 되지만 순위선택 방법에서는 순위가 매겨지게 되며 부모로 선택될 확률이 생기게 되어 무게 제한을 만족하는 개체만 필터링하는 코드를 추가해야 했습니다.
# 순위 선택
def rank_selection(population):
ranked_population = sorted(population, key=fitness, reverse=True) # 적합도 순위
rank_weights = [len(ranked_population) - rank for rank in range(len(ranked_population))] # 높은 순위에 가중치 부여
total_rank = sum(rank_weights)
probabilities = [w / total_rank for w in rank_weights]
return random.choices(ranked_population, probabilities, k=2)# 순위 선택 (필터링 추가)
def rank_selection(population):
# 무게 제한을 만족하는 개체만 필터링
valid_population = [ind for ind in population if fitness(ind) > 0]
if not valid_population: # 유효한 개체가 없을 경우 전체 개체 사용
valid_population = population
ranked_population = sorted(valid_population, key=fitness, reverse=True)
rank_weights = [len(ranked_population) - rank for rank in range(len(ranked_population))]
total_rank = sum(rank_weights)
probabilities = [w / total_rank for w in rank_weights]
return random.choices(ranked_population, probabilities, k=2)
'AI' 카테고리의 다른 글
| [논문리뷰] ALCM: Autonomous LLM-Augmented Causal Discovery Framework (7) | 2025.07.23 |
|---|---|
| [Causal Analysis] PC 알고리즘 (1) | 2025.03.30 |
| 효과적인 프롬프트 엔지니어링 (기초) : 프롬프트 구성요소와 효과적인 프롬프트 구조 (0) | 2025.03.02 |
| LLM 기법(Fine-tuning, RAG) 설명 및 적용 가이드 (0) | 2025.02.16 |
| [LLM] Fine-tuning시 early stopping 적용하기 (1) | 2024.03.14 |